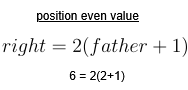Why Heaps Work: The Mathematics Behind Priority Queues
A heap is a priority queue data structure organized in the form of a tree, in which the root node contains the element with the highest priority. This priority may correspond to either the minimum or maximum value, depending on the desired configuration (min-heap or max-heap).
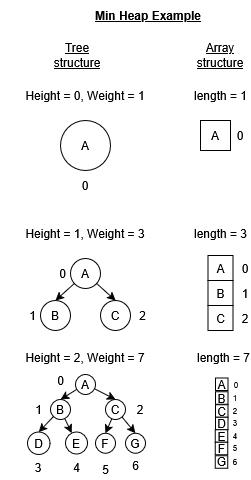
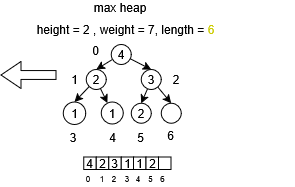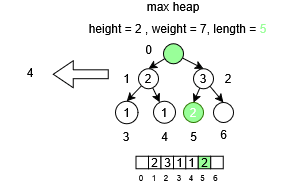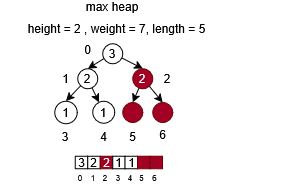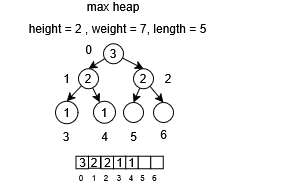
Furthermore, due to its binary growth, it is possible to determine both the height and the weight (number of nodes) of the tree with precision, which facilitates the analysis of its behavior and computational complexity. As shown in the following image, three heap trees of different heights are presented, allowing for an efficient increase in the number of elements stored in the array:
In addition, due to its binary growth, it is possible to accurately determine the height based on the weight (number of nodes) of the tree:
On the other hand, the previous equation can be rearranged to determine the height from the weight:
The weight of the tree is one of the most important attributes of the structure, as it indicates the amount of memory space being used, while the height provides an estimate of the processing time. Therefore, both concepts can be combined and, based on heuristics, optimal values can be determined according to the application context.
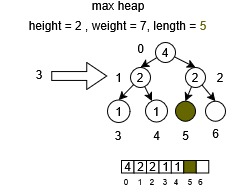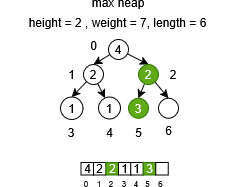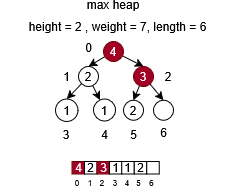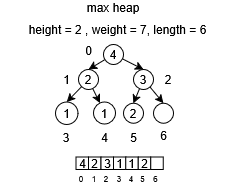
For example, in a monetary application, it has been determined that within one minute there may be a maximum demand of 100 transactions. In this scenario, prioritizing high-value monetary transactions is required; therefore, the engineers designed a max heap with a height of 6 to meet this demand while also providing capacity for up to 27 additional transactions.
Searching for patterns in a perfect binary tree
In the previous section, it was observed that the heap corresponds to a perfect tree. However, this structure can be represented using a linear structure, specifically an array, which allows the establishment of a lexicographic mapping to directly access the position of each node.
To construct this mapping, it is noted that left child nodes occupy odd positions within the array. Consequently, based on the general expression that defines odd numbers, it is possible to compute the position of the left child using the current position of the parent node. For example, if the parent node is located at position 2, its left child is found at position 5.
On the other hand, right child nodes correspond to even positions. Similarly, by applying the expression that characterizes even numbers, the position of the right child can be determined. Following the same example, for a parent node located at position 2, the right child is found at position 6.
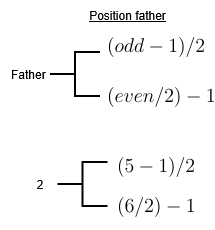
Based on the previous equations, it is possible to derive the position of the father node from the position of the current node, taking into account whether the index is even or odd and greater than zero. This restriction is necessary because the root node is located at position zero and, therefore, does not have a parent.
Heap operations
Once the fundamental concepts of the heap are established, it can be deduced that it provides two essential operations. The push method allows the insertion of elements while maintaining the priority order dynamically during execution. Conversely, the pop operation returns the element with the highest priority without compromising the integrity of the priority structure.
Push method
The implementation of the push operation is straightforward. Initially, the value to be inserted is placed at the last position of the array. Subsequently, the algorithm traverses the structure upward by identifying the parent node of the current position and verifying whether the child node holds a higher priority value than its parent. If this condition is satisfied, the values of the parent and child nodes are exchanged. This process is repeated iteratively from the updated position until no further exchanges are required or the root node is reached.
Pop function
For the implementation of the pop operation, the priority element located at the root node is removed from the structure. Subsequently, the last inserted element in the array is moved to the root position. The algorithm then traverses the structure downward by identifying the left and right child nodes of the current position. If either child possesses a higher priority than the parent node, their values are exchanged. This process continues iteratively until no further exchanges are required or a leaf node is reached.
Conclusion
In conclusion, the heap tree is a priority-based data structure in which elements are organized according to their priority, allowing insertion and retrieval operations to be performed with logarithmic time complexity. However, it is important to consider that the structure may encounter limitations if it grows excessively, since the height of the tree increases logarithmically with the number of nodes, which can impact performance in very large datasets. Additionally, defining the priority value is crucial, and it can be determined based on various business requirements or solution-specific criteria.